Đối với hình tam giác được phân ra thành một số loại chính như: tam giác thường, tam giác vuông, tam giác cân, tam giác đều, tam giác vuông cân… Xét cụ thể công thức tính chu vi và diện tích của từng hình tam giác.
CT tính chu vi tam giác
Chu vi tam giác thường
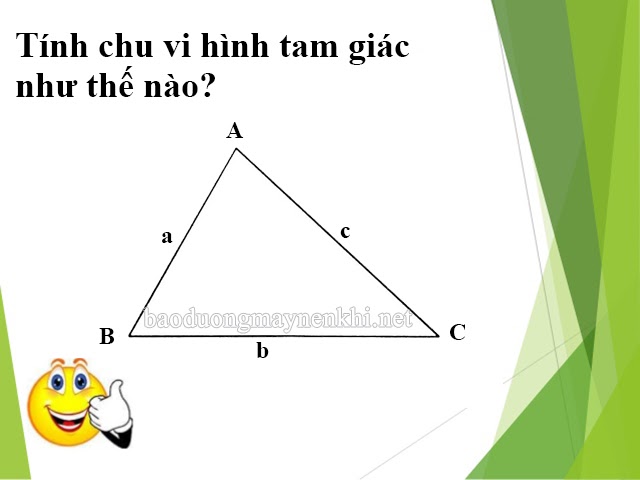
Với đặc điểm là loại tam giác cơ bản nhất, độ dài và số đo góc của tam giác này cũng có sự chênh lệch. Cách tính chu vi tam giác thường đó là bạn cộng độ dài của 3 cạnh lại. Ví dụ đối với tam giác ABC có độ dài cạnh AB = a, BC = b và AC = c. Lúc này, chu vi kí hiệu là P sẽ được biểu diễn dưới dạng như sau:
P = a+b+c
Trường hợp bạn muốn tính nửa chu vi tam giác thì giá trị lúc này sẽ là:
P/2 = (a+b+c)/2
Chu vi tam giác vuông
Tam giác vuông là tam giác có số đo một góc bằng 90 độ. Khi đó, công thức tính chu vi tam giác vuông sẽ bằng tổng số đo của hai cạnh góc vuông và cạnh huyền.
P = a+b+c
Trong đó:
-
- a, b lần lượt là hai cạnh hợp thành góc vuông đó
- c là cạnh huyền, hay cạnh đối diện góc vuông.
Chu vi tam giác cân
Tam giác cân có hai cạnh bên có độ dài bằng nhau, do đó công thức tính chu vi tam giác cân như sau:
P = 2a+c
Trong đó:
-
- a là cạnh bên của tam giác cân. 2a tương ứng với tổng của hai cạnh bên
- c là cạnh đáy.
Công thức tính chu vi tam giác cân trong hệ Oxyz cũng có thể áp dụng đối với tam giác vuông cân vì thực chất là những giá trị này là bằng nhau.
Chu vi tam giác đều
Đối với tam giác đều có 3 cạnh bằng nhau thì công thức tính chu vi được thực hiện như sau:
P = 3a
Trong đó:
-
- a là chiều dài của cạnh tam giác (Vì độ dài là như nhau nên có thể viết dạng tích là 3a)
Công thức tính diện tích tam giác thường, đều, cân, vuông cân
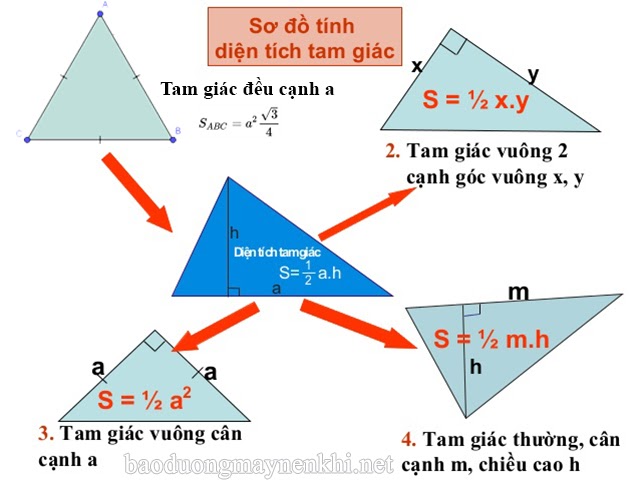
Công thức tính diện tích tam giác thường
Công thức tính diện tích tam giác thường trong Oxyz được tính bằng ½ tích giữa chiều cao hạ từ một đỉnh của tam giác nhân với độ dài cạnh đối diện.
Xét với tam giác ABC có độ dài cạnh AB = a, BC = b, AC = c, chiều cao AH là h. Vậy diện tích tam giác công thức như thế nào?
Lời giải:
Dựa theo phát biểu chung nhất về cách tính diện tích tam giác như trên thì ta có dạng như sau:
S = (c.h)/2
Trường hợp biết một góc trước, ví dụ như biết góc BAC thì công thức diện tích được áp dụng theo kiến thức lớp 8 như sau:
S = (a.b.sin ACB)/2
Trong đó:
- a, b lần lượt hai cạnh hợp thành góc BAC
- Bạn có thể thực hiện tương tự khi biết số đo góc và độ dài hai cạnh hợp thành khác.
Diện tích tam giác đều
Công thức tính diện tích tam giác đều có 3 cạnh bằng nhau, cùng bằng a thì bạn có thể áp dụng theo định lý Heron:
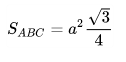
Công thức tính diện tích tam giác cân
Cho tam giác cân ABC cạnh AB = AC = a, tính diện tích tam giác cân cạnh a? Trước hết, bạn thực hiện việc nối một chiều cao AH = h từ đỉnh A xuống cạnh BC. Lúc này, công thức tính sẽ được biểu diễn là:
S = a.h/2
Trường hợp tam giác vuông cân tại đỉnh A, cách tính diện tích tam giác vuông cân được thực hiện như sau:
S = a2/2
Công thức tính diện tích tam giác vuông
Tam giác vuông ABC có độ dài hai cạnh góc vuông AB, AC lần lượt là a và b. Công thức tính lúc này sẽ là:
S = a.b/2
5 công thức tính diện tích tam giác nâng cao
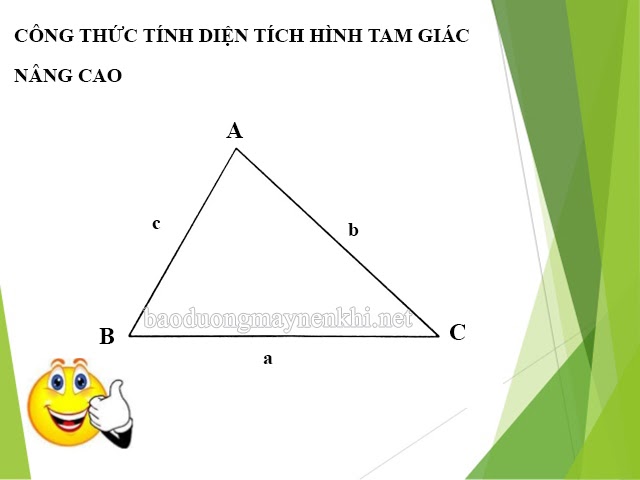
Thực chất việc học các công thức tính diện tích các loại tam giác được học ngay từ lớp 3, lớp 5, tuy nhiên đến lớp 8 thì người học lại được cập nhật thêm các cách tính nâng cao hơn.
Ví dụ: Cho tam giác ABC có độ dài BC = a, AC = b, AB = c. Chiều cao hạ từ các đỉnh A, B, C lần lượt là ha, hb, hc. Diện tích tam giác được áp dụng theo các công thức lần lượt là:
- Công thức 1
S = (a. ha)/2 = (a. hb)/2 = (a. hc)/2
- Công thức 2
S = (a.b.sinC)/2 = (b.c.sinA)/2 = (c.a.sinB)/2
- Công thức 3
Áp dụng công thức Heron như sau:

Trong đó: p là nửa chu vi của tam giác. p = (a+b+c)/2
- Công thức 4
S = p.r
Trong đó: r là bán kính đường tròn nội tiếp tam giác
- Công thức 5
Diện tích tam giác ABC trong Oxyz có A(xA,yA),B(xB,yB),C(xC,yC) sẽ là:
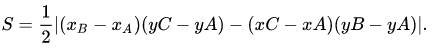
Trên đây là những kiến thức tổng hợp về công thức tính diện tích, chu vi tam giác là gì? Hy vọng với những thông tin này có thể giúp ích bạn trong việc tính toán thực tế như: tính chu vi, diện tích tam giác đều, thường, vuông hay cân…



